Prikaz številk na ravnini (definicija)

2024 Avtor: Leah Sherlock | [email protected]. Nazadnje spremenjeno: 2023-12-17 05:48

Zmožnost pravilnega prikaza različnih oblik na ravnini lista, platna in katere koli druge površine je precej pomembna veščina. Predvsem pa je pomemben tako za ljudi umetnosti: slikarje, kiparje, grafike, oblikovalce (notranjih prostorov in arhitekturnega okolja), kot za ljudi znanosti: matematike, fizike, oblikovalce, izumitelje.

Pomembno pa je tudi, da se oseba, ki je daleč od teh sfer, nauči pravilno zaznati in prikazati svet okoli sebe. To pomaga razumeti veliko globlje vso njegovo vsestranskost. Če nimate zadostne ideje, kako to narediti pravilno, vam najverjetneje ne bo uspel projekt, slika ali risba katerega koli izuma. To pomeni, da je ta veščina pomembna tako za reševanje preprostih, vsakdanjih nalog kot za tiste, ki imajo globalni, univerzalni pomen.

Malo zgodovine

Že od antičnih časov so ljudje poskušali upodobiti, kar so videli okoli sebe: druge ljudi, nekaj primitivnih zgradb tistih časov, neverjetno lep svet rastlin in živali, veličastne gore in preprosto stvari, gospodinjske predmete. Se pravi svet v vsej svoji raznolikosti in veličini.

A takrat še niso imeli pojma, kako je to mogoče narediti natančno in kompetentno, tako da je bil prikaz različnih tridimenzionalnih predmetov na ravnini res realističen, živ. Oseba ni imela ustreznega znanja, poleg tega pa ni bilo posebnih veščin, razen morda najosnovnejših.

V prejšnjih virih je rečeno, da je bila prva slika na svetu sestavljena iz ene črte, ki je potekala vzdolž sence osebe, ki jo je na steno oddalo sonce. Se pravi, narava je sama predlagala, v katero smer se je vredno premakniti v iskanju prave rešitve tega vprašanja.

In to vprašanje je tedanjega človeka skrbelo tudi iz tega razloga: ni hotel le občudovati obsežne žive silhuete, tako rekoč izvirne, ampak je želel ujeti prostorski objekt na ravnini. In to je storil zato, da je na ta način lahko okrasil svoj dom ali zanj sveto mesto ali pa vzel s seboj snop s sliko in ga premaknil na poljubno razdaljo.

Geometrija vzorca

In karkoli že rečeš, a minila so leta, stoletja in nekako so se, ko se je civilizacija razvijala, ljudje postopoma naučili prikazovati kompleksne figure v dvodimenzionalnem prostoru, torej na ravnini. Šele zdaj se je natančnost velikosti in razmerij upodobljenih predmetov začela zdeti zelo približna.

Toda vprašanje, kako pravilen je prikaz figure na ravnini in koliko ustrezajo volumnu prvotnih predmetov, je nekoč postalo zelo pomembno. Na nek način je nova znanost imenovanageometrijo. Natančneje, njen odsek je deskriptivna geometrija.

Tukaj samo preučuje oblike in ravnine, črte in točke, pa tudi njihov odnos med seboj - tako v tridimenzionalnem kot v dvodimenzionalnem prostoru.

Načini pretvorbe

Pomembna značilnost vizualne umetnosti je prikaz figur na slikovni ravnini. Navsezadnje gre pravzaprav za zajemanje tridimenzionalnih prostorskih objektov v dvodimenzionalnosti. Namreč: kompleks je treba pretvoriti v enostavnega, torej je treba predmet, ki ima dolžino, širino, višino, prenesti na ravnino.

In deskriptivna geometrija naredi takšne "prehode" zahvaljujoč nekaterim metodam. Skupno jih je približno šest. Tu so trije glavni in najbolj priljubljeni po vsem svetu:

• perspektiva (ko je upodobljeni predmet odstranjen v prostoru);
• ortogonalna projekcija (vzporedna projekcija, kjer so žarki pravokotni na ravnino);
• poševna projekcija (vzporedna projekcija, kjer so žarki nagnjeni glede na ravnino).

Upodobljeni predmet se pojavi precej jasno v aksonometrični projekciji (ki vključuje pravokotno in poševno). Toda najbolj jasno in resnično se projicira, ko je prikazano v perspektivi. In prav zgornje metode v veliki meri rešujejo vprašanje, kako prikazati številke na ravnini.

Perspektiva

Perspektiva zaseda najbolj častno mesto med drugimi metodami slikanja. Ker človeško okokot objektiv fotoaparata na podoben način vidi okoliški prostor. Stvari, ki so bolj oddaljene od opazovalca, se zdijo manjše in včasih veliko manjše, kot če so blizu.

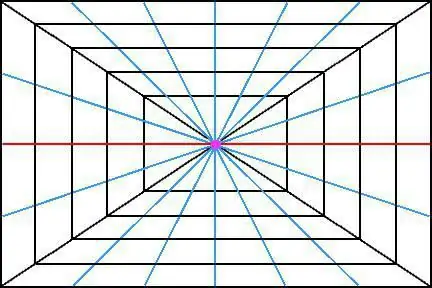
Na primer vzemite sliko kocke v vesolju. Če so v resnici vsi njeni robovi vzporedni drug z drugim, se lahko, ko pogledate ta predmet v daljavi, zdi, da se robovi zbližajo (ali bi se morali) v eni točki. In kar je najbolj zanimivo, ne smejo se le zbližati na eni točki, ampak imeti eno samo presečišče.

Zahvaljujoč mojstrom renesanse: Albrechtu Dürerju, Pieru Della Francescu, Andrei Mantegni, Leonu Batisti Albertiju, moderno slikarstvo ve, kaj je neposredna linearna perspektiva, kako določiti višino obzorja in izginjajoče točke.

In svetovno znani genij - Leonardo da Vinci - je prvi utemeljil koncept zračne perspektive. To vključuje spremembo barve, tona predmeta, spremembe njegovih kontrastnih značilnosti (zmanjšanje, ko se predmet odmika).

Ortografska projekcija

Ortogonalna se imenuje vzporedna projekcija, ki je usmerjena na ravno črto, ki je pravokotna na ravnino. V procesu njegove uporabe ostanejo dimenzije obrisov predmeta nespremenjene. To pomeni, da je predmet prikazan brez popačenja.

Projicirani tridimenzionalni objekt je tako rekoč razstavljen na tri poglede: od strani, od spredaj in od zgoraj. In če pogledate vse to hkrati, lahko dodatepredstavitev, kako je predmet videti po volumnu. Hkrati ostanejo dimenzije figure nespremenjene tako na tridimenzionalni sliki kot na dvodimenzionalni.

Poševna projekcija

Ta projekcija je razdeljena na več podvrst, in sicer:

• izometrični pogled;
• dimetrična projekcija;
• trimetrična projekcija.

Izometrična ima koeficiente popačenja v vseh 3 oseh (dolžina, širina, višina). To pomeni, da so koti med parno vzetimi osemi enaki 120 stopinj. V dimetričnem so popačenja vzdolž 2 osi enaka, tretja pa je drugačna. In v trimetrični projekciji so vsi koeficienti popačenja (torej vzdolž vseh 3 osi) različni.

Oblike vrtenja

Ko se pravokoten trikotnik vrti vzdolž osi enega od dveh krakov, bo njegova tretja stranica (hipotenuza) opisala novo figuro, imenovano stožec. In če pravokotnik (kvadrat) zavrtite vzdolž ene od njegovih strani, dobite valj. Ko se polkrog zavrti, se bo pojavila krogla.

Iz tega sledi, da z vrtenjem ravnine vzdolž neke osi dobimo tako imenovane figure vrtenja.

Te figure imajo vrtilno os. Kako izgledajo v ravnini, je odvisno od njihove postavitve glede na višino oči. Na primer, zgornja in spodnja stran valja sta v bistvu krogi. In če jih pogledaš v letalu, so videti kot elipse.

Toda naloga postane še težja, če pri prikazovanjuprostorske figure na ravnini, imajo nagnjeno os. Pomembno je, da so konture vrtilnih teles enako oddaljene od osi slednjih.

Malo o chiaroscuro

Chiaroscuro igra pomembno vlogo pri prikazovanju številk na letalu. Ker volumen upodobljenega predmeta nastane ne le zaradi črt, temveč tudi zaradi pravilne porazdelitve svetlobe in sence na njegovih straneh. In potem je videti precej obsežno v ravnini dvodimenzionalne površine.

Tako je prikaz številk na ravnini, določanje njihovih velikosti, značilnosti pravilnega prekrivanja svetlobnih in temnih madežev zaradi zgornjih metod povsem mogoč. In kar je najpomembneje, to so resnično preverjene metode v praksi, ki jih uporabljajo vodilni strokovnjaki našega časa.